一、什么是高等数学？

初等数学--研究对象为常量，以精致观点研究问题。

高等数学--研究对象为变量，运动和辩证法进入了数学。

数学中的转折点是笛卡尔的变数。有了变数，运动进入了数学，有了变数，辩证法进入了数学，有了变数，微分和积分也就立刻成为必要的了，而它们也就立刻产生。--恩格斯

主要内容：

1、分析基础：函数，极限，连续

2、微积分学：一元微积分（上册）、多元微积分（下册）

3、向量代数与空间解析几何

4、无穷级数

5、常微分方程

二、如何学习高等数学？

1、认识高等数学的重要性，培养浓厚的学习兴趣。

一门科学，只有当他成功地运用数学时，才能达到真正完善的地步。--马克思

要辩证而又唯物地了解自然，就必须熟悉数学。--恩格斯

2、学数学最好的方式是做数学。

聪明在于学习，天才在于积累。学而优则用，学而优则创。由薄到厚，由厚到薄。--华罗庚

第一章 函数与极限

分析基础：函数--研究对象

                 极限--研究方法

                 连续--研究桥梁

第一节 映射与函数

一、集合

1、定义及表示法

定义1、具有某种特定性质的事物的总体称为集合。组成集合的事物称为元素。

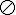空集，

元素a属于/不属于集合M,记作,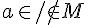

注：M为数集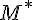：排除0的数集

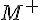                       排除0和负数的数集

表示法：（1）列举法 （2）描述法

2、集合之间的关系及运算

定义2 包含关系：A是B的子集，B包含A

空集是任意集合的子集

B包含A，C包含B，则C包含A

A包含B，B包含A，则A=B

定义3 运算：并集、交集、差集、余集、直积

二、映射

三、函数

11111111

N  :自然数集  Z 整数集  Q 有理数集合  R 实数集合

满射： 每一个y都有一个对应原像 

单射：

双射：（1对1）既是满射又是单射

集合：

元素：

空集：

1.函数极限，

集合

组成集合的事物称为元素，没有元素成为去空集

解决变速问题，科学运用数学时，才能达到完善，学习的最后方法是做数学。由薄到厚，由厚到薄（运用）

函数与极限

研究对象是函数，方法是极限，连续是桥梁

（壹）

具有某种特定性质的东西

集合不一定是数

什么是高等数学

常量

变量

速度于匀速运动，函数，极限，连续，

学习代数的重要性

1.培养兴趣

2.因为当科学运用数学时，才能达到完美的地步。

要辩证法，学数学做数学

一·什么是高等数学

1. 高等数学研究的对象是变量，运动和辩证法，以运动的观点来看问题。
2.  

高等数学

第01讲

第一章  函数与极限

分析基础：

• 函数 — 研究对象
• 极限 — 研究方法
• 连续 — 研究桥梁

第一节 映射与函数

一、集合

集合：具有某种特定性质的事物的总体称为集合，组成集合的事物称为元素。

高等数学研究的是函数，极限是工具

高等数学：

1.函数与极限

学而优则优

N  自然数       1，2,3，4

Z   整数           -1,0,1

Q  有理数        -1，,0，1，½（整数和分数）

R   实数            有理数和无理数

Z 包含N   Q包含Z     R包含Q

    海伦公式：S=根号下[p(p-a)(p-b)(p-c)]=1/4根号下[(a+b+c)(a+b-c)(a+c-b)(b+c-a)]，

这其中，a，b，c是三角形的三边的长度，p=（a+b+c）/2

高等数学与初等数学的区别：后者是靓包止的观点看问题，前者是用运动的观点看问题。初等数学解决匀加速问题，不涉及变量问题。变量问题引入辩证法观点，学函数函数习数学就有了自己的看法、引入函数与极限和微分，解决实际问题。

第一章  函数与极限

研究的对象是函数，方法是极限，连续是连接两者的桥梁。

第一节   映射与函数

1、集合：具有一定事物特定性质的总体

组成集合的个体，称为元素

不含任何元素的集合，称为空集

元素用小写字母，集合用大写字母

N: 自然数集

Z: 整数集合

Q: 有理数集合

R: 实数集合

72个课时，一元微积分

70个课时左右，多元微积分

函数--研究的对象

极限--研究的方法

连续--研究的桥梁

映射：满射，单射，双射（一 一映射）逆映射

                           函数与极限

分析基础：

1）函数-研究对象

2）极限-研究方法

3）连续-研究桥梁

第一节:映射与函数

一.集合

二.映射

三.函数

------------------------------------------------

一：集合

1.集合的概念，用大写的字母表示。

2.元素的概念，用小写的字母表示。

3.集合之间的关系及运算

点1：属于关系{

自然数集合 属于 整数集合

N ∈ Z

整数集合 有理数

Z∈Q

有理数集合 实数集合

Q∈R

}

点2：并集，交集，差集，余集，直积关系

{

并集：A∪B

交集：A ∩ B

差集：A\B || A-B

余集：A-B（B∈A）

直积：A*B

}

二：映射

1.映射的概念

1）映射的三要素-定义域，对应规则，值域

2）元素x的像y是唯一的，但是y的原像不一定唯一。