1.若x->x0时,函数f(x)->0,则函数f(x)为x->x0是的无穷小
说明:除0意外任何很小的常数都不是无穷小
2.无穷大:若任给M>0,总存在德尔塔>0,使对一切满足不等式0<|x-x0|<德尔塔的x,总有|f(x)|>M,则称函数f(x)当x-x0时为无穷大
3.无穷下与无穷大的关系:
在自变量的同一变化过程中,若f(x)为无穷大,则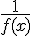 为无穷小,若f(x)为无穷小,且f(x)不等于0,则
为无穷小,若f(x)为无穷小,且f(x)不等于0,则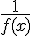 为无穷大
为无穷大
1.若x->x0时,函数f(x)->0,则函数f(x)为x->x0是的无穷小
说明:除0意外任何很小的常数都不是无穷小
2.无穷大:若任给M>0,总存在德尔塔>0,使对一切满足不等式0<|x-x0|<德尔塔的x,总有|f(x)|>M,则称函数f(x)当x-x0时为无穷大
3.无穷下与无穷大的关系:
在自变量的同一变化过程中,若f(x)为无穷大,则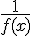 为无穷小,若f(x)为无穷小,且f(x)不等于0,则
为无穷小,若f(x)为无穷小,且f(x)不等于0,则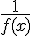 为无穷大
为无穷大
无穷小:函数自变量在x---x0的变化过程中,函数极限为零; 其实为极限等于零的一种情况。
从头再学一次的时候,才发觉,数学原来的美还是需要被发现的。
无穷小是接近于0,但是不等于0, 如果limf(x)=A,那么f(x)=A+a,其中lima=0 只有lima=0时,f(x)=A+a才成立 反之如果f(x)=A+a,且lima=0,那么limf(x)=A 既然lima=0了,所以limf(x)=A 不是等于常数A+a,是无限趋近,就像.当N趋于无穷大的时候1/N就趋近于0,也就说无限接近。
第四节
无穷小与无穷大
一、无穷小
二、无穷大
三、无穷大与无穷大的关系